Lingkaran adalah sekumpulan titik yang sama jarak dari satu titik. Koordinat titik-titik ini ditentukan oleh susunan persamaan pekeliling. Ini ditentukan berdasarkan panjang jejari dan koordinat pusat bulatan.
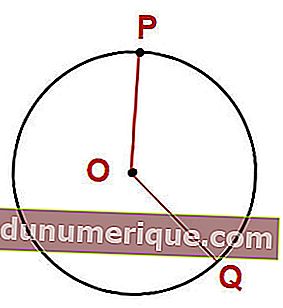
Dalam gambar di atas, kita dapat menyimpulkan bahawa OP = OQ. Titik O disebut pusat bulatan, sementara OP dan OQ adalah jari-jari. Mari kita perhatikan contoh berikut.
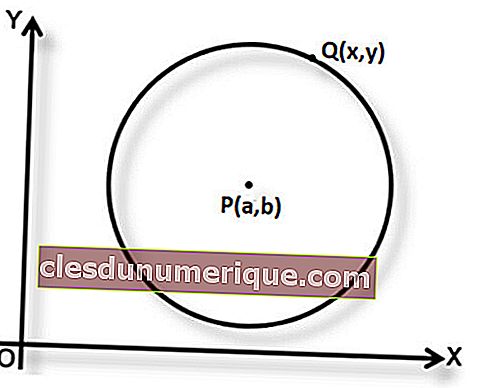
P (a, b) adalah pusat bulatan dan panjang jejari adalah r. Sekiranya Q (x, y) adalah titik yang terletak pada bulatan, berdasarkan definisi bulatan dapat disimpulkan bahawa PQ = r. Dari ini, kita dapat merumuskan persamaan bulatan dengan P (a, b) sebagai pusat dan r sebagai jejari.
√ (x - a) 2 + (y - b) 2 = r
(x - a) 2 + (y - b) 2 = r2
Mari kita atasi masalah contoh di bawah.
Cari persamaan bagi bulatan yang pusatnya berada pada titik (-5,4) dengan radius 7!
Dari penyataan ini, kita tahu bahawa a = -5, b = 4, dan r = 7. Sekiranya kita memasukkannya ke dalam persamaan, kita mendapat jawapan berikut.
(x - (-5)) 2 + (y - 4) 2 = 72
(x + 5) 2 + (y - 4) 2 = 49
Bagaimana dengan lingkaran yang koordinat pusatnya berada pada P (0,0)? Persamaan bagi bulatan adalah seperti berikut.
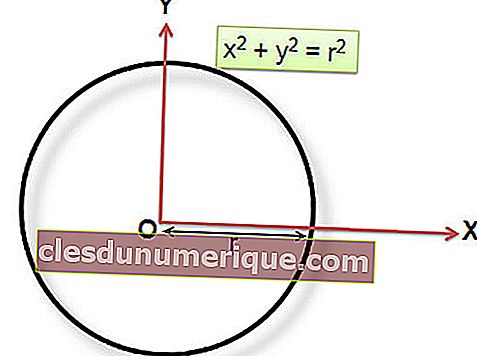
Bentuk umum persamaan pekeliling dapat dinyatakan dalam bentuk berikut.
(x - a) 2 + (y - b) 2 = r2, atau
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, atau
X2 + y2 + Px + Qy + S = 0, di mana P = -2a, Q = -2b, dan S = a2 + b2 - r2
Syarat untuk Menentukan Persamaan Bulatan
Persamaan bulat mengandungi tiga pemboleh ubah sewenang-wenangnya. Persamaan bulatan dapat ditentukan sekiranya nilai ketiga pemboleh ubah tersebut diketahui. Untuk mengetahui nilai ketiga pemboleh ubah ini, salah satu syarat berikut mesti dipenuhi:
- Koordinat tiga titik pada bulatan diketahui.
- Koordinat dua titik pada bulatan yang dihubungkan dengan diameter bulatan diketahui.
- Koordinat titik tengah dan koordinat titik pada bulatan diketahui.