Sekiranya anda belajar matematik, anda pasti pernah mendengar atau mempelajari trigonometri. Nah, trigonometri adalah cabang matematik yang mengkaji hubungan antara sudut dan panjang sisi segitiga, misalnya, seperti sinus, kosinus, dan tangen. Secara harfiah, trigonometri berasal dari bahasa Yunani, iaitu trigonon yang bermaksud "tiga sudut" dan metron, yang bermaksud "untuk mengukur". Seperti pelbagai bahan dalam matematik, terdapat formula trigonometri yang perlu anda ketahui.
Pada kesempatan ini, kami akan berusaha memahami pelbagai jenis formula dan juga contoh masalah mereka.
Rumusan Trigonometri
Konsep trigonometri adalah konsep penting dalam segitiga. Nilai trigonometri dirumuskan berdasarkan nisbah panjang sisi segitiga kanan. Terdapat enam nilai nisbah trigonometri, iaitu sinus (sin), cosine (cos), tangent (tan), cosecant (cosec), secant (sec), dan cotangent (cot). Enam jenis nilai trigonometri dapat ditentukan dengan membandingkan panjang sisi dengan peraturan tertentu.
Penggunaan trigonometri adalah banyak, mulai dari astronomi, geografi, teori muzik, akustik, analisis pasaran kewangan optik, elektronik, teori kebarangkalian, statistik, biologi, pengimejan perubatan, farmasi, kimia, dan banyak lagi.
Jadi, sekarang adalah masa untuk kita mengenali pelbagai formula trigonometri dalam pelajaran ini.
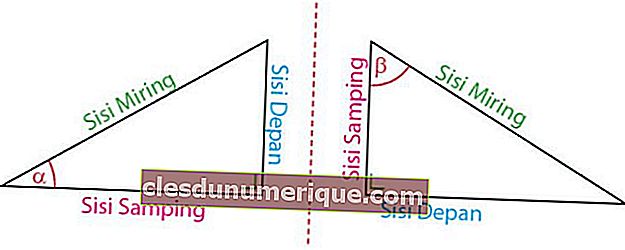
Sumber Imej: idschool.net
Berdasarkan lokasinya ke sudut, sisi segitiga - siku dibahagikan kepada tiga jenis, iaitu sisi depan, sisi sisi, dan hipotenus. Bahagian depan adalah sisi yang menghadap ke sudut. Bahagiannya berada di sisi sudut. Bahagian miring selalu berada di hadapan sudut 90o.
Nah, tiga fungsi trigonometri utama adalah fungsi sin, cos, dan tan. Definisi tiga fungsi berdasarkan sisi dan sudut segitiga kanan dapat dilihat pada rajah dan persamaan di bawah.
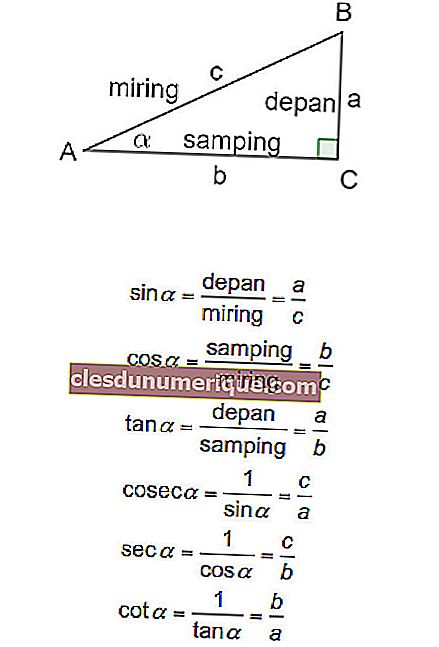
Sekarang, khusus untuk sudut khas, nilai trigonometri adalah seperti berikut:
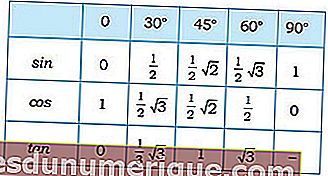
Sumber Imej: madematics.net
Perbandingan Trigonometri Sudut Berkorelasi
Nisbah trigonometri sudut yang berkaitan adalah perpanjangan nilai trig asas yang ditentukan dari sudut segitiga tepat. Sudut segitiga kanan hanya pada kuadran I kerana sudut akut yang ukurannya 0 ° - 90 °.
Sudut tengah bulatan adalah antara 0 ° - 360 °. Sudut dibahagikan kepada 4 kuadran, setiap kuadran mempunyai jarak 90 °.
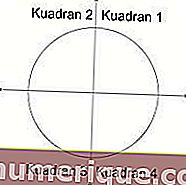
Sumber gambar: studiobelajar.com
- Kuadran 1 mempunyai sudut antara 0 ° - 90 °. Semua nilai nisbah trigonometri positif pada kuadran ini.
- Kuadran 2 mempunyai sudut antara 90 ° - 180 °. Dalam kuadran ini, hanya nilai sinus dan kosekant yang positif.
- Kuadran 3 mempunyai sudut antara 180 ° - 270 °. Dalam kuadran ini, hanya tangen dan kotoran yang positif.
- Kuadran 4 mempunyai sudut antara 270 ° - 360 °. Dalam kuadran ini, hanya kosinus dan sekuat positif.
Identiti Trigonometri
Teorema Pythagoras, iaitu a2 + b2 = c2 adalah asas untuk penyediaan identiti trigonometri. Identiti trigonometri menyatakan hubungan fungsi trigonometri dengan fungsi trigonometri yang lain.
Jumlah kuasa dua sinus dan kuasa dua kosinus sama dengan satu. Sekiranya kedua-dua belah belah dibahagi dengan kuasa dua kosinus, satu tambah dengan kuasa dua sama dengan segiempat sama. Begitu juga, jika kedua-dua belah belah dibahagi dengan sinus kuadrat, kita boleh mendapatkan satu ditambah kuadrat kuadrat sama dengan kosecan kuasa dua.
Inilah formula identiti:
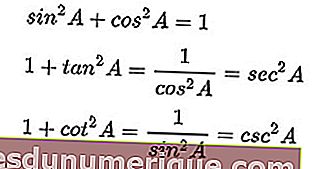
Sumber Imej: wikipedia.org
Pelbagai Rumusan Lain
Terdapat formula lain yang harus anda ketahui, iaitu:
Rumus untuk jumlah dan perbezaan sudut:
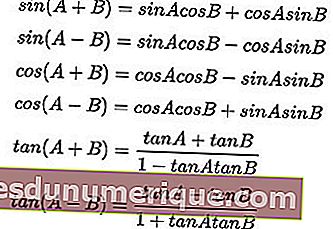
Formula Pendaraban Trigonometri:
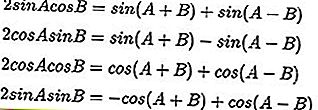
Rumus dan Perbezaan Trigonometrik
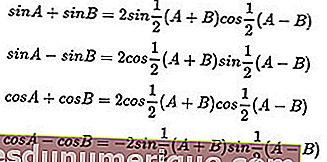
Contoh Masalah Trig
Cari nilai 2 kos 75 ° kos 15 °:
Penyelesaian:
Berdasarkan maklumat dalam masalah tersebut, kita dapat melihat bahawa masalah di atas merangkumi pendaraban trigonometri. Gunakan formula pendaraban untuk cos yang dijelaskan di atas, iaitu 2 cos A cos B = cos (A + B) + cos (A - B).
Jawapan:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75 - 15) °
= cos 90 ° + cos 60 °
= 0 + ½
= ½
Itulah koleksi formula dan masalah trigonometri yang boleh anda pelajari dan fahami. Untuk dapat memahaminya dengan lebih baik, anda boleh mencuba MASALAH, penyelesaian dalam talian yang berwajaran, lengkap untuk mempraktikkan soalan sesuai dengan kurikulum terkini di Kelas Pintar. Bermula dari peringkat sekolah rendah, sekolah menengah hingga sekolah menengah dengan pelbagai mata pelajaran seperti Matematik, Fizik, Kimia dan lain-lain. Di sini anda dapat mempelajari pelbagai jenis formula lengkap dengan masalah contoh,
Ayuh, tunggu apa lagi! Mari cuba latihan MASALAH di Kelas Bestari sekarang