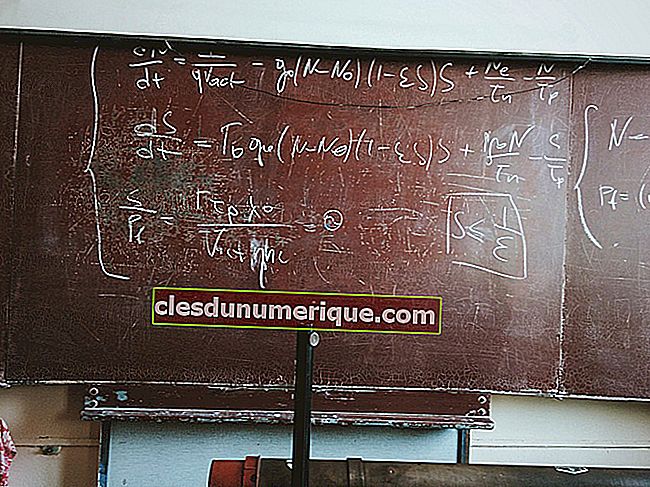Pernahkah anda menyaksikan pertembungan antara dua kenderaan di lebuh raya? Apa yang berlaku apabila dua kenderaan bertembung? Jika dilihat dari fizik, perlanggaran itu membawa maut atau tidak ditentukan oleh momentum kenderaan. Untuk memahami lebih lanjut mengenai ini, mari kita pelajari bahan mengenai momentum dan dorongan.
Dalam fizik, momentum didefinisikan sebagai kuantiti yang dimiliki oleh objek bergerak. Jumlah momentum akan bergantung pada jisim dan halaju objek. Secara matematik, momentum boleh ditulis sebagai p = mv, di mana p adalah momentum (kg m / s), m adalah jisim objek (kg) dan v adalah halaju objek (m / s).
Berdasarkan formula ini, dapat dilihat bahawa momentum sebanding dengan halaju objek. Oleh itu, arah momentum sama dengan arah halaju, selain itu semakin besar halaju suatu objek semakin besar momentumnya.
Sementara itu, dorongan adalah hasil daya rata-rata dan selang masa daya bertindak. Secara matematik, dorongan boleh ditulis sebagai I = FΔt, di mana saya adalah dorongan dalam ns, F adalah daya yang diberikan dalam Newton, dan Δt adalah selang waktu dalam beberapa saat.
Hubungan Impuls dan Momentum
Hubungan antara impuls dan momentum dijelaskan oleh teorem impuls-momentum. Teorema impuls-momentum menyatakan bahawa dorongan yang bertindak pada objek sama dengan perubahan momentum objek.
(Baca juga: Ketahui 3 Klasifikasi Bahan)
Berdasarkan undang-undang kedua Newton menyatakan bahawa daya (F) yang diberikan pada suatu objek sama dengan perubahan momentum (Δp) unit dalam masa (Δt). Secara matematik, hubungan antara dorongan dan perubahan momentum dapat ditulis seperti berikut: I = Δp = p2 - p
Hukum Kekebalan Momentum
Hukum kekebalan momentum menyatakan bahawa jika tidak ada daya luaran yang bertindak pada sistem maka momentum objek sebelum dan selepas perlanggaran adalah sama. Ini bermaksud bahawa momentum total sistem objek sebelum perlanggaran selalu sama dengan momentum total sistem objek selepas perlanggaran. Secara matematik, hukum kekebalan momentum boleh ditulis seperti berikut: m1v1 + m2v2 = m1v1 ′ + m2v2 ′
Maklumat:
Di mana m1 adalah jisim objek
m2 ialah jisim objek 2
v1 ialah halaju objek 1 sebelum perlanggaran
v2 adalah halaju objek 2 sebelum perlanggaran
v1 'adalah halaju objek 1 selepas perlanggaran
v2 'adalah halaju objek 2 selepas perlanggaran.
Perlanggaran
Perlanggaran boleh dibahagikan kepada tiga jenis, iaitu perlanggaran berdaya tahan sempurna, perlanggaran ketahanan separa dan perlanggaran tidak berdaya tahan sepenuhnya. Untuk menentukan jenis perlanggaran, dapat dilihat dari nilai pekali pemulihan, yang merupakan nilai negatif perbandingan antara halaju relatif kedua-dua objek selepas perlanggaran dan sebelum perlanggaran. Secara matematik, nilai pekali pemulihan boleh ditulis seperti berikut:
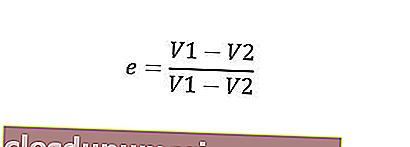
Nilai pekali pemulihan untuk tiga jenis perlanggaran adalah:
Dalam perlanggaran yang berdaya tahan sempurna, nilai e =
Dalam perlanggaran separa, 0 <e <
Dalam perlanggaran tidak berdaya tahan, e = 0