Aljabar, yang kita pelajari dalam bab berjudul bentuk aljabar, adalah cabang matematik di mana dalam menyelesaikan masalah, angka digantikan dengan huruf. Perkataan aljabar itu sendiri diambil dari bahasa Arab "al-jabr" yang bermaksud "mengumpulkan bahagian yang patah". Istilah ini diambil dari tajuk buku Ilm al-jabr wa'l-muḳābala oleh ahli matematik dan ahli astronomi Parsi, Al-Khwarizmi.
Pada mulanya, aljabar disebut prosedur pembedahan penyesuaian patah tulang atau dislokasi. Makna matematik itu sendiri pertama kali dicatat pada abad ke-16.
Aljabar dibentuk oleh gabungan huruf dan angka. Bentuk yang dipisahkan oleh tanda tambah disebut suku kata; huruf dalam bentuk algebra disebut pemboleh ubah; nombor yang dilampirkan pada pemboleh ubah dipanggil pekali; sementara nombor tanpa pemboleh ubah disebut pemalar. Istilah yang mempunyai pemboleh ubah yang sama dengan kuasa yang sama disebut istilah seperti
(Baca juga: Ketahui Jenis Matriks, Apa Itu?)
2y + 3−4x + y, misalnya. Ini adalah bentuk aljabar, dengan pekali 2, -4, dan 1. Pemboleh ubahnya adalah x dan y. Pemalar adalah 3, sementara sebutan serupa dalam bentuk di atas adalah 2y dan y.
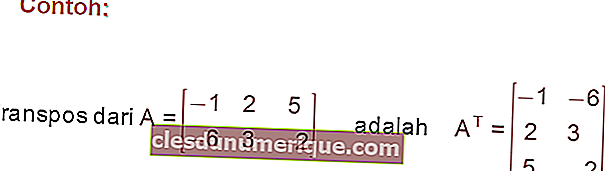
Contoh: Seekor burung terbang 500 meter dalam satu minit. Bolehkah anda menuliskan jarak yang ditempuh oleh burung berbanding masa penerbangannya dalam beberapa minit?
Jumlah masa dalam minit adalah t
Kemudian, jumlah jarak = halaju (v) x masa (t)
s = 500 xt = 500t meter
Dalam ilustrasi di atas, kita boleh menganggap beberapa kuantiti seperti b dan t dikenali sebagai pemboleh ubah. Kita juga boleh menggunakan huruf lain sebagai pemboleh ubah, seperti x, y, z dan lain-lain.
Operasi Algebra
Di Algebra, kami menyedari bahawa terdapat empat operasi aritmetik yang dapat digunakan, termasuk penambahan, pengurangan, pendaraban, dan pembahagian.
Penambahan
Istilah yang boleh ditambah dalam bentuk aljabar adalah seperti istilah. Penambahan borang ini dapat dilakukan dengan menambahkan pekali dengan pekali atau pemalar dengan pemalar dalam istilah yang sama tanpa mengubah pemboleh ubah.
Contoh: 5ab + 3ab + 2ab = (5 + 3 + 2) ab = 10ab
"Gabungan pekali dengan pemboleh ubah dan pemalarnya yang berkaitan dengan sekurang-kurangnya satu operasi aritmetik seperti +, -, x, atau: dikenali sebagai bentuk aljabar"
Penolakan
Istilah yang boleh dikurangkan dalam bentuk algebra adalah seperti istilah. Mengurangkan bentuk ini boleh dilakukan dengan mengurangkan pekali dari pekali atau pemalar dengan pemalar dalam istilah yang sama tanpa mengubah pemboleh ubah.
(Baca juga: Logik Matematik, dari Negasi hingga Biimplikasi)
Contoh: 6ab - 3ab = (6−3) ab = 3ab
Pendaraban
Pendaraban dalam bentuk algebra dapat diselesaikan dengan kaedah distributif. Dalam pendaraban algebra, kekuatan pemboleh ubah akan ditambah.
4 (x + y) = 4.x + 4.y = 4x + 4y
2x (x + y) = 2x.x + 2x.y = 2 × 2 + 2xy
(x + y) (2x + y) = x.2x + x.y + y.2x + yy
= 2 × 2 + xy + 2xy + y2
= 2 × 2 + 3xy + y2
(x - y) (2x + y - z) = x.2x + x.y + x. (- z) + (- y) .2x + (- y) .y + (- y). (- z)
= 2 × 2 + xy - xz - 2xy - y2 + yz
Bahagian
Pembahagian bentuk algebra satu istilah dapat dilakukan dengan mengira hasil tambah pekali dengan pekali dan pemboleh ubah dengan pemboleh ubah. Dalam pembahagian pemboleh ubah, kekuatan pemboleh ubah akan dikurangkan. Sementara itu, untuk pembahagian lebih dari satu penggal, ia boleh menggunakan kaedah berjenjang.
Contoh:
8a2b: 4ab = (8: 4) a2−1b1−1 = 2a
6x3y2z: 3xy3z2 = (6: 3) x3−1y2−3z1−2 = 2x2y - 1z−