Adakah anda memberi perhatian, jika bumbung rumah dan khemah hampir sama bentuknya? Sekiranya anda melihat semula, sepertinya terdiri daripada 2 segitiga di setiap hujungnya, kemudian ditutup dengan selimut yang berbentuk segi empat tepat. Bentuk ini juga dikenali sebagai prisma segitiga. Ini disebut kerana pangkal dan penutupnya berbentuk segitiga. Dalam geometri, kita akan mengkaji definisi dan formula prisma segitiga. Pada kesempatan ini kita juga akan membincangkan pelbagai contoh masalah agar dapat memahami bahan ini dengan lebih mendalam.
Prisma adalah bentuk yang mempunyai penutup dan dasar dengan bentuk sisi-n yang kongruen, sementara sisi menegak berbentuk segi empat tepat.
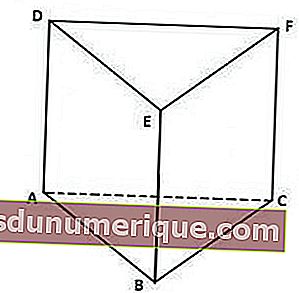
Prisma segitiga mempunyai ciri-ciri berikut:
Mempunyai asas segitiga dan penutup yang serasi.
Dari gambar di atas, penutup prisma, iaitu segitiga DEF, mempunyai bentuk dan ukuran yang sama dengan segitiga ABC dengan dasarnya.
Segi empat tepat sebagai sisi menegak.
Anda dapat lihat, prisma di atas dibatasi oleh tiga segi empat tepat pada setiap sisi menegak, iaitu segi empat tepat ACFD, BCFE, dan ABED.
Mempunyai 5 sisi, 9 tepi, dan 6 bucu.
5 sisi prisma segitiga terdiri daripada 1 sisi pangkal, 1 sisi penutup dan 3 sisi menegak. Manakala 9 tulang rusuk terdiri daripada 3 tulang rusuk tegak, 3 sisi pangkal, dan 3 sisi penutup. Juga, 6 bucu adalah titik A, B, C, D, E, dan F.
Sekarang, setelah kita mengetahui ciri-ciri dan juga makna prisma segitiga, inilah masanya bagi kita untuk mengetahui formula prisma segitiga dan contoh masalahnya.
Rumusan Prisma Segitiga dan Masalah Contoh
Akan ada 2 jenis formula prisma segitiga yang kita pelajari. Rumus untuk mencari isipadu, dan formula untuk mencari luas permukaan. Rumusannya seperti ini:
Isipadu
Untuk isi padu, kami akan menggunakan formula:
V = luas pangkal × tinggi
atau
V = (½ x a x h) × tinggi prisma
Oleh itu, untuk memahami perkara ini dengan lebih baik, mari kita lihat contoh masalah yang satu ini:
Prisma setinggi 10 cm. Pangkal prisma berupa segitiga kanan dengan panjang sisi masing-masing 4cm dan 3cm. Berapakah isipadu prisma segitiga ini?
Penyelesaian:
Di sini, kita hanya perlu memasukkan nombor yang diketahui ke dalam formula seperti ini:
V = (½ x a x h) × tinggi prisma
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Kawasan permukaan
Dalam mengira luas permukaan prisma segitiga, kita akan menggunakan formula seperti ini:
L = (2 x luas pangkalan) + (luas semua sisi tegak lurus)
jika segi tiga sama sisi, maka anda boleh menggunakan formula:
L = (2 x luas pangkalan) + (3 x luas satu sisi menegak)
Atau boleh jadi formula:
L = (2 x luas pangkalan) + (perimeter asas x tinggi prisma)
Mari lihat contoh masalah yang satu ini untuk melihat bagaimana formula ini diaplikasikan. Berikut adalah contoh masalahnya:
Terdapat prisma segitiga sama sisi yang mempunyai ketinggian 12 cm, panjang sisi 5 cm dan tinggi 8 cm. Lalu, apakah luas permukaan prisma segitiga ini?
Penyelesaian:
Untuk mencari luas permukaan, kita hanya menggunakan formula untuk luas permukaan prisma segitiga seperti ini:
L = (2 x luas pangkalan) + (3 x luas satu satah menegak)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
Jadi itulah pelbagai formula prisma segitiga yang harus anda ketahui, serta beberapa contoh masalah. Sekiranya anda masih keliru, anda boleh bertanya di ruangan komen atau anda boleh mencuba Smart Class, platform bimbingan dalam talian yang dipercayai di Dunia.









