Sekadar makluman, hubungan juga wujud dalam matematik, anda tahu. Hubungan wujud dalam bahan mengenai set. Hubungan adalah peraturan yang menghubungkan ahli set dengan anggota kumpulan yang lain. Hubungan dari set A ke set B menghubungkan anggota set A dengan anggota set B. Dalam kesempatan ini kita akan belajar mengenai contoh hubungan dan sifatnya, serta pelbagai contoh masalah yang dapat membantu anda memahami bahan ini dengan lebih baik.
Contoh Hubungan dan Sifatnya
Hubungan boleh didefinisikan sebagai peraturan yang menghubungkan anggota kawasan asal (domain) dan anggota kawasan persahabatan (codomain). Dalam hubungan, tidak ada peraturan khusus yang harus dipatuhi untuk memadankan anggota persatuan daerah dengan anggota daerah yang ramah.
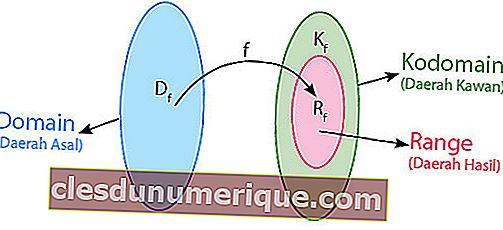
sumber: idschool.net
Setiap anggota persatuan serantau boleh mempunyai lebih daripada satu pasangan atau sama sekali tidak mempunyai pasangan. Hubungan dua set dapat dinyatakan dalam tiga cara, iaitu:
- Gambar rajah anak panah
- Gambarajah Cartesian.
- Kumpulan pasangan berturut-turut
Berikut adalah penjelasan lebih lanjut mengenai tiga cara:
Carta Anak Panah
Carta anak panah adalah kaedah termudah untuk menyatakan hubungan. Gambar rajah ini akan membentuk corak hubungan dalam bentuk anak panah yang menunjukkan hubungan dari anggota set A dengan anggota set B.
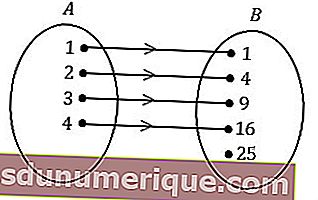
Sumber: maretong.com
Gambarajah Cartesian
Gambarajah Cartes adalah gambarajah yang terdiri daripada paksi X dan paksi Y. Dalam rajah Cartesian, anggota set A terletak pada paksi X, sementara anggota set B terletak pada paksi Y. Hubungan yang menghubungkan set A ke B ditunjukkan oleh titik atau titik.
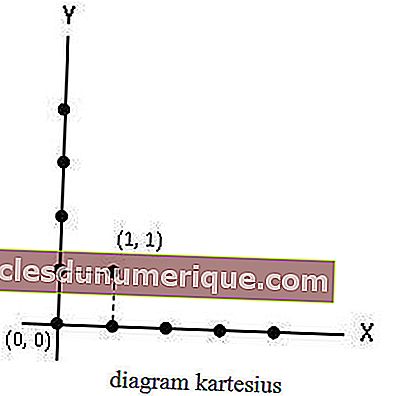
Set pasangan berturut-turut
Hubungan yang menghubungkan satu set dengan set yang lain dapat ditunjukkan dalam bentuk satu set pasangan teratur. Cara penulisannya ialah anggota set A ditulis terlebih dahulu, sementara anggota set B yang merupakan pasangan ditulis kedua.
Contoh seperti ini:
A = Set dunia, Jepun, Korea, Perancis
Set B = Tokyo, Paris, Jakarta, Seoul
Tentukan set pasangan tertib mengikut negara dan ibu negara.
Jawapan:
{(Dunia, Jakarta), (Jepun, Tokyo), (Korea, Seoul), (Perancis, Paris)}
Fungsi
Fungsi atau pemetaan adalah hubungan khusus dari set A hingga set B, dengan peraturan bahawa setiap anggota set A dipadankan tepat satu dengan anggota set B.
Hasil pemetaan dari domain ke domain disebut rentang fungsi atau kawasan hasil. Sama seperti hubungan, fungsi juga dapat ditunjukkan dalam bentuk diagram anak panah, pasangan tertib dan diagram Cartesian.
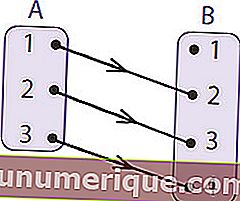
Sumber: rumushitung.com
Untuk memahaminya lebih jauh, pertimbangkan gambar di atas. Kumpulan A atau kawasan asal disebut domain. Set B yang merupakan kawasan rakan dipanggil codomain. Anggota kawasan ramah yang merupakan hasil pemetaan disebut kawasan hasil atau julat fungsi. Maka dari rajah anak panah di atas dapat disimpulkan bahawa
- Domain (D f) ialah A = {1,2,3}
- Codomain ialah B = {1,2,3,4}
- Julat / Hasil (R f) ialah = {2,3,4}
Fungsi boleh dilambangkan dengan huruf kecil seperti f, g, h, i, dan sebagainya. Fungsi peta f menetapkan A ke set B, maka ia dapat dilambangkan dengan f (x): A → B.
Contohnya ialah fungsi f yang memetakan A hingga B dengan peraturan f: x → 2x + 2. Dari notasi fungsi, x adalah ahli domain. Fungsi x → 2x + 2 bermaksud fungsi f memetakan x hingga 2x + 2. Jadi luas x dengan fungsi f adalah 2x + 2. Oleh itu, anda boleh menandakannya menjadi f (x) = 2x +2.
Sekiranya fungsi f: x → ax + b dengan x adalah anggota domain f, maka formula untuk fungsi f adalah
f (x) = kapak + b
Contoh masalah:
Diberi fungsi f: x → 2x - 2 di mana x adalah integer. Cuba tentukan nilai f (3).
Penyelesaian:
Fungsi f: x → 2x - 2 dapat diwakili oleh f (x) = 2x - 2
jadi,
f (x) = 2x - 2
f (3) = 2 (3) - 2 = 4
Jadi itulah contoh hubungan dan fungsi dalam matematik. Adakah anda mempunyai pertanyaan mengenai perkara ini? Tuliskan soalan anda di ruangan komen, dan jangan lupa untuk berkongsi pengetahuan ini.









