Siapa yang suka ais krim? Lebih-lebih lagi ais krim yang menggunakan kon. Ia sangat sedap, sejuk dan manis juga. Oleh itu, pernahkah anda terfikir berapa jumlah ais krim yang harus diisi ke dalam kon sehingga penuh? Adakah ada yang tahu bagaimana mengira isipadu ais krim ini? Wow, jika tidak, ini adalah peluang bagi anda untuk mempelajari formula untuk isipadu kerucut dan juga cara menghitungnya.
Tetapi, sebelum kita menyelidiki formula untuk jumlah kerucut dan juga cara mencarinya, mari kita ketahui apa itu kerucut. Kerucut adalah salah satu ruang sisi melengkung. Ia mempunyai pangkal bulat dan selimut yang menghubungkan pangkal dan titik atas.
Kerucut itu juga mempunyai 3 ukuran penting yang akan kita gunakan untuk mengira isipadu, iaitu:
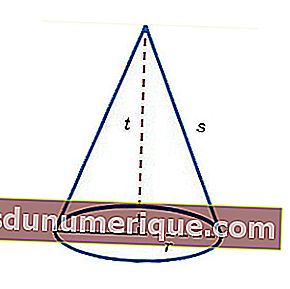
1. Radius Cone
Pangkal kerucut berbentuk bulatan. Jejari atau jejari kon adalah jarak antara titik tengah ke titik pada bulatan asas. Diameter dasar kerucut adalah segmen yang menghubungkan dua titik pada bulatan asas dan melalui titik tengah. Dalam bulatan, diameter bulatan sama dengan dua kali jejari bulatan.
2. Ketinggian Kerucut
Adakah jarak antara pusat pangkal dan bucu kon. Sekiranya kita membuat segmen garis yang menghubungkan titik pusat asas dan bucu, kita akan mendapat segmen garis yang berserenjang dengan satah dasar. Panjang segmen ini juga tinggi kon.
3. Selimut Kerucut
Selimut kon adalah sisi melengkung, membungkus kerucut. Ia terletak di antara pangkalan dan titik atas. Di dalam selimut kon terdapat garis-garis pelukis. Garis pelukis adalah garis yang mewakili selimut terluar kon. Garis pelukis, ketinggian kerucut, dan jejari kon membentuk segitiga tepat.
Selain daripada unsur-unsur di atas, kita juga harus mengetahui ciri-ciri bentuk kerucut, iaitu:
- Kon mempunyai satu sisi.
- Kon mempunyai satu bucu.
- Kerucut tidak mempunyai tulang rusuk.
- Kerucut mempunyai jaring dalam bentuk lingkaran dan grid bulat.
Sekarang mari kita masuk ke formula untuk isipadu kerucut, dan juga cara mengira.
Formula Isipadu Kerucut
Dalam mengira isipadu kerucut, kami akan menggunakan formula satu ini:
V = 1/3 x π x r2 xt
Maklumat:
v = isipadu kon
t = tinggi kon
r = jejari pangkal kon
Kami akan menggunakan π = 22/7 jika jejari (r) atau diameter (d) adalah gandaan 7 atau dibahagi dengan 7.
Kami akan menggunakan π = 3.14 jika jejari (r) atau diameter (d) bukan gandaan 7 atau tidak boleh dibahagi dengan 7.
Mari kita lihat contoh masalah yang satu ini untuk lebih memahami cara mencari isi padu kerucut.
Soalan:
Kon mempunyai jejari asas 10 cm dan tinggi 20 cm. Berapakah isi padu kerucut itu?
Penyelesaian:
Kita hanya perlu memasukkan nombor ke dalam formula, seperti ini:
V = 1/3 x π x r2 xt
V = 1/3 x 3.14 x 10cm2 x 20cm
V = 2,093.33 cm3
Sekiranya anda merasa masih memerlukan lebih banyak soalan untuk memahami bahan ini, anda boleh memanfaatkan produk PROB dari Smart Class. Dalam produk ini terdapat pelbagai jenis soalan latihan untuk anda belajar menjadi lebih stabil dalam menghadapi peperiksaan. Merangkumi masalah mengenai kon. Terdapat juga fitur PERTANYAAN yang dapat diakses secara percuma dan untuk menjawab pertanyaan mengenai pertanyaan atau bahan yang belum dikuasai. Soalan anda dijawab dengan segera oleh guru dan mentor yang disahkan.
Jadi itulah sedikit perbincangan mengenai formula isi padu kerucut yang harus anda ketahui. Sekiranya anda masih keliru, tuliskan soalan anda di ruangan komen.









