Adakah anda pernah melihat pergerakan pada bandul atau spring? Dua pergerakan yang anda perhatikan dikelaskan sebagai pergerakan harmonik sederhana. Ia adalah pergerakan berulang-alik di sekitar titik keseimbangan. Sekiranya anda memperhatikan, bandul mempunyai titik keseimbangan di tengahnya, kerana walaupun kelajuannya menurun, bandul masih akan bergerak di sekitar titik keseimbangan.
Gerakan harmonik sederhana mempunyai amplitud tetap (sisihan maksimum) dan frekuensi. Gerakan ini berkala. Setiap pergerakan akan berlaku berulang kali dan berkala pada selang waktu yang sama.
Dalam gerakan harmonik sederhana, daya yang dihasilkan mempunyai arah yang sama, iaitu menuju titik keseimbangan. Daya ini dipanggil daya pemulihan. Jumlah daya pemulihan berkadar terus dengan kedudukan objek hingga titik keseimbangan.
Beberapa ciri gerakan ini termasuk grafik kedudukan zarah sebagai fungsi masa dalam bentuk sinus atau kosinus. Gerakan ini juga dapat dilihat dari persamaan penyimpangan, persamaan halaju, persamaan halaju, dan persamaan tenaga gerakan yang dimaksudkan.
(Baca juga: Kuantiti dalam Konsep Gerak Lurus)
Berdasarkan ciri-ciri ini, gerakan harmonik sederhana mempunyai penyimpangan, halaju, pecutan, dan tenaga.
Penyimpangan
Penyimpangan harmonik sederhana boleh dianggap sebagai unjuran zarah bergerak dalam bulatan biasa pada diameter bulatan. Secara umum, persamaan penyimpangan dalam gerakan ini adalah seperti berikut.
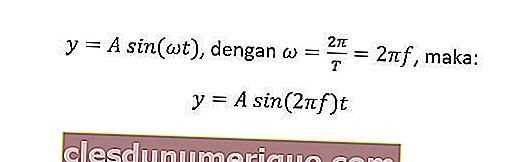
y = penyimpangan getaran (m)
ω = halaju sudut (rad / s)
T = tempoh
f = kekerapan (Hz)
t = masa perjalanan
A = amplitud / sisihan maksimum (m)
Kepantasan
Kelajuan adalah turunan kedudukan pertama. Dalam gerakan harmonik sederhana, halaju diperoleh daripada turunan pertama persamaan sisihan. Persamaan halaju dapat dijelaskan seperti berikut.

Pecutan
Pecutan suatu objek bergerak harmonik sederhana dapat diperoleh dari derivatif pertama dari persamaan halaju atau terbitan kedua dari persamaan sisihan. Persamaan pecutan dapat diperoleh seperti berikut.
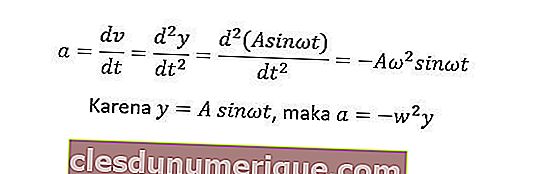
Sisihan maksimum mempunyai nilai yang sama dengan amplitud (y = A), jadi pecutan maksimum adalah am = - Aw
Tenaga
Persamaan tenaga dalam gerakan harmonik sederhana merangkumi tenaga kinetik, tenaga berpotensi, dan tenaga mekanikal. Tenaga kinetik objek dapat dirumuskan seperti berikut.
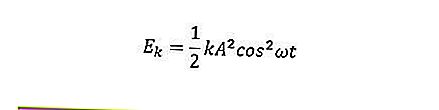
Tenaga berpotensi objek dapat dirumuskan seperti berikut.
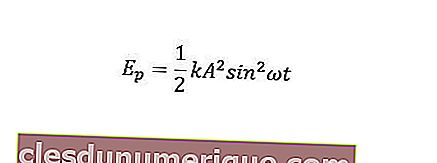
Sementara itu, tenaga mekanikal adalah jumlah tenaga kinetik dan tenaga berpotensi.
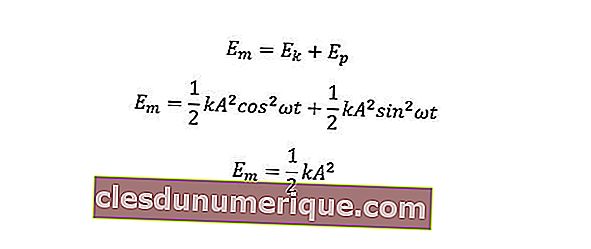
k = nilai tetap (N / m)
ω = halaju sudut (rad / s)
A = amplitud (m)
t = masa perjalanan
Jumlah tenaga berpotensi dan tenaga kinetik objek yang bergerak harmonik sederhana selalu tetap.